1級電気工事施工管理技士 過去問
令和7年度（2025年）
問1 (午前 イ 問1)

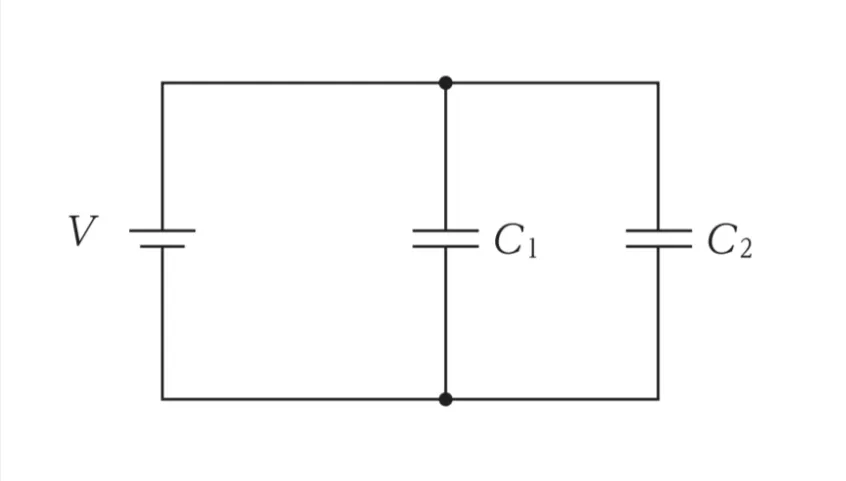
この図では、2つのコンデンサC1とC2が直流電源に対して並列に接続されています。

こうした場合、個々のコンデンサに蓄えられたエネルギーを足すことで合計のエネルギーを求めることができます。

コンデンサに蓄えられるエネルギーU（J）は以下のように求めることができます。

　（1/2×コンデンサの静電容量C(F)×コンデンサにかかる電圧Vの2乗）

    U=1/2×C×V ^2

　この公式を用いて計算すると、　C1には100μジュール　C2には200μジュールのエネルギーが蓄えられることになり

合計して300μジュールとなります。　　300μジュール　すなわち300×10^-6　

つまり3×10^-4となります。　

コンデンサの回路で、コンデンサに蓄えられる合計エネルギー値を求める問題です。

コンデンサは、並列につながっているため、C1とC2の合成静電容量C0は、

C0＝C1+C2＝2＋４＝6 [μF]

です。

C0に蓄えられた電荷Qは、Q＝C0×Vです。

コンデンサに蓄えられるエネルギーW [J]は、

W＝(1/2)Q×V＝(C0×V²)／2＝6×100／2＝300 μJ

＝3×10²×10^－6 [J]

＝3×10^－４ [J]