1級電気工事施工管理技士 過去問
令和7年度(2025年)
問3 (午前 イ 問3)
問題文
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
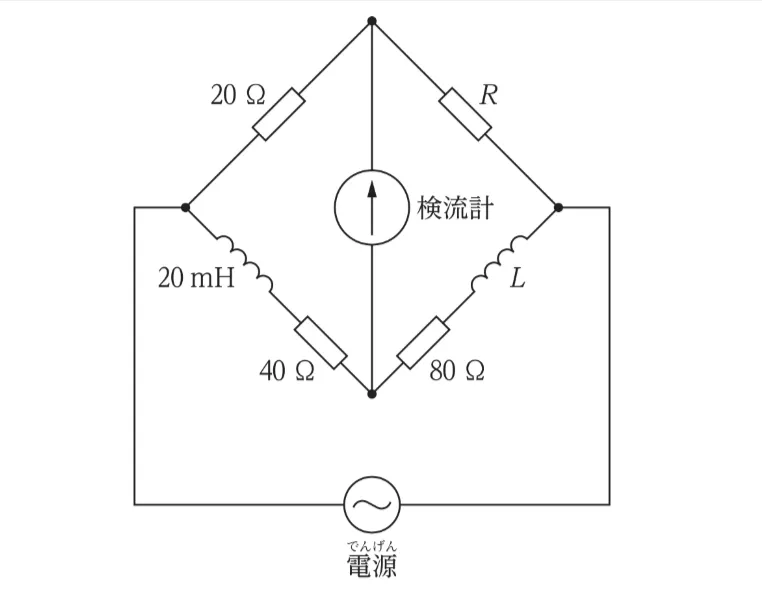
問題
1級電気工事施工管理技士試験 令和7年度(2025年) 問3(午前 イ 問3) (訂正依頼・報告はこちら)

- (R)10Ω (L)40mH
- (R)40Ω (L)40mH
- (R)60Ω (L)20mH
- (R)80Ω (L)80mH
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
これは、ホイートストンブリッジ回路の交流における平衡条件の理解を問う問題です。
直流回路においては、抵抗だけを考慮して
中央の四角形の回路の向かい合う辺の抵抗値を掛け合わせた数値が、
別の向かい合う辺の抵抗値を掛け合わせた数値と等しければ、
回路は平衡し、検流計の置かれている部分の電流がゼロになります。
交流回路においても、基本的に同様の考え方ですが、抵抗成分に加え、リアクタンス成分も釣り合っている必要があります。
まず抵抗成分だけに注目すると左上が20Ωで、右下が80Ωですから、
この組み合わせの掛け合わせた数値は20×80=1600になります。
これに対して左下の抵抗は40Ωで、右上のRの抵抗値が問われており、
回路は平衡している(検流計指示が0)のため、以下の式が成り立ちます。
40×R=1600
これからR=40Ωと計算できます。
次にリアクタンス成分に注目しますが、この釣り合いは、リアクタンス部だけではなく、回路中の抵抗にも影響されます。
設問の図において 左下の20mHのコイルをL1とし、左上の20Ωの抵抗をR1とした場合、
コイルLの大きさは、右上の抵抗Rも含めて以下のように表せます。
L=(R/R1)×L1
既に求めているR=40Ωも含めて、実際の数値を代入すると計算式は以下のようになります。
L=(40/20)×20mH
計算すると、L=40mHとなります。
この結果、R=40Ω L=40mH となる選択肢が正解です。
参考になった数11
この解説の修正を提案する
02
交流ブリッジ回路を構成する、抵抗とインダクタンスの値を求める問題です。
図に交流ブリッジを示します。
図では、ab間のインピーダンスをZ1、電流をI1とし、同様に各辺のインピーダンスと電流を記述しています。
インピーダンスは、上に●を付けて、複素数で表しています。(ただし、この解説では省略します)
交流ブリッジが、平衡になると、次の条件が成立します。
・ab間に電流が流れず、電流検知Dは、0となります。
・Z1×Z4=Z2×Z3 が成立します。
問題図では、検流計の指示値が0であることから、ブリッジ回路は平衡条件にあります。
Z1×Z4=Z2×Z3 が成立することから、次のように計算を進めます。
Z1=20 、Z2=R 、Z3=40+jω(20×10-3)、Z4=80+jω(L×10-3)
20×(80+jω(L×10-3))=R×(40+jω(20×10-3))
1600+jω(20L×10-3)=40R+jω(800×10-3)
実数部と虚数部が等しくなるため、
1600=40R
20L×10-3=800×10-3
R=1600/40=40 [Ω]
L=800/20=40 [mH]
誤
R=40 Ωです。Lは合っています。
正
冒頭の解説どおりの結果です。
誤
R=40、L=40 です。
誤
R=40、L=40 です。
参考になった数1
この解説の修正を提案する
前の問題(問2)へ
令和7年度(2025年) 問題一覧
次の問題(問4)へ