1級電気工事施工管理技士 過去問
令和7年度（2025年）
問6 (午前 イ 問6)

　有効電力・無効電力・皮相電力・力率の理解を求める問題です。

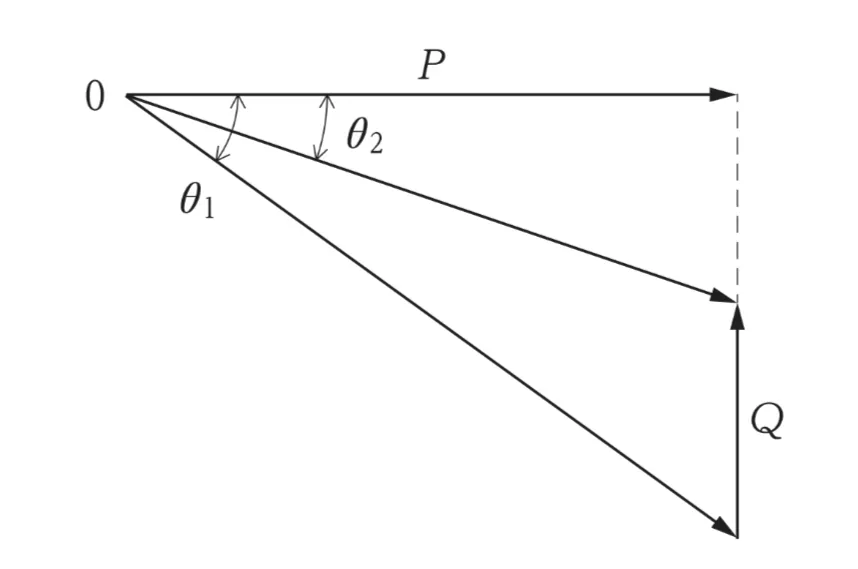
　この設問の図で、有効電力は横軸、無効電力は縦軸で示され、その2つを合成した斜辺の線が皮相電力にあたります。

　そして力率は有効電力である横軸と皮相電力の斜線との角度であり、θ１もしくはθ２で示されています。

　問題文で、三相負荷の初期状態での有効電力Pが1200kW、cosθ1が０．６とありますから、

　初期状態の皮相電力をS1とすると、P÷S1= cosθ1であることになります。

　この式をS1について解くと、S1=2000kVAであることが分かります。

　そして直角三角形の斜辺にあたるS1が2000、底辺となるＰが1200ですから、残る高さとなる無効電力は、三平方の定理より求めることができます。

　初期状態の無効電力をQ1とすれば、（Q1）^２=（S1）^２－(P)^２となりますから、Ｐ=1200およびS1=2000を代入し計算すると

Q1=1600kvarと求められます。

　次にコンデンサを接続した時に力率が0.8に改善されたわけですが、この状況での無効電力をQ2とし、皮相電力をS2とすれば、

　P÷S2= cosθ2　つまり　1200÷S2=0.8　となります。

　これをS2について解くと、S2=1500kVAと分かります。

　また、S2(1500kVA)を斜辺、底辺をＰ(1200kＷ)とする直角三角形での高さ（Q2とする）は、

　（Q2）^２=（S2）^２－（P）^２　で表すことができ、Ｐ=1200およびS2=1500を代入し計算すると

Q2=900kvarと求められます。

　コンデンサを接続することで、1600kvarだった無効電力が、900kvarになったというわけですから、

コンデンサの容量は、1600－900=700kvarとなります。

三相負荷に並列に進相コンデンサを接続して力率を改善したときに、進相コンデンサの容量を求める問題です。

計算前に、tanθ1、tanθ2を求めます。

sinθ1＝√(1－0.6²)＝0.8より、tanθ1＝0.8/0.6＝1.33

sinθ2＝√(1－0.8²)＝0.6より、tanθ2＝0.6/0.8＝0.75

有効電力に対しての力率と無効電力の関係を、下図に示します。

力率0.6のときの無効電力Q1 [kvar]は、P＝1200 [kW]から、

Q1＝P×tanθ1＝1596 [kvar]

力率改善後の力率0.8のときの無効電力Q2 [kvar]は、

Q2＝P×tanθ2＝900 [kvar]

力率改善に要するコンデンサ容量Q [kvar]は、

Q ＝ Q1－Q2 ＝ 1596－900 ≒ 700 [kvar]